Impedanz oder Scheinwiderstand Z
In der Gleichstromtechnik gibt es nur Wirkwiderstände. In der Wechselstromtechnik kommen nun Blindwiderstände (Induktivitäten und Kapazitäten) hinzu, an welchen Blindleistung umgesetzt wird.
Der sogenannte Scheinwiderstand bezeichnet den Gesamtwiderstand aus Wirk- und Blindwiderständen.
In der Wechselstromtechnik herrscht zwischen Strom und Spannung an einem passiven Zweipol (z.B. Widerstand, Spule, Kondensator) meist eine Phasenverschiebung. Diese Phasenverschiebung wird mit dem Winkel \( \varphi \) angegeben, wobei der Strom immer die Bezugsgröße ist:
\( \varphi=\varphi_u-\varphi_i \)
Wenn \( \varphi \) größer als 0 ist, dann eilt die Spannung dem Strom voraus.
Wenn \( \varphi \) kleiner als 0 ist, dann eilt der Strom der Spannung voraus.
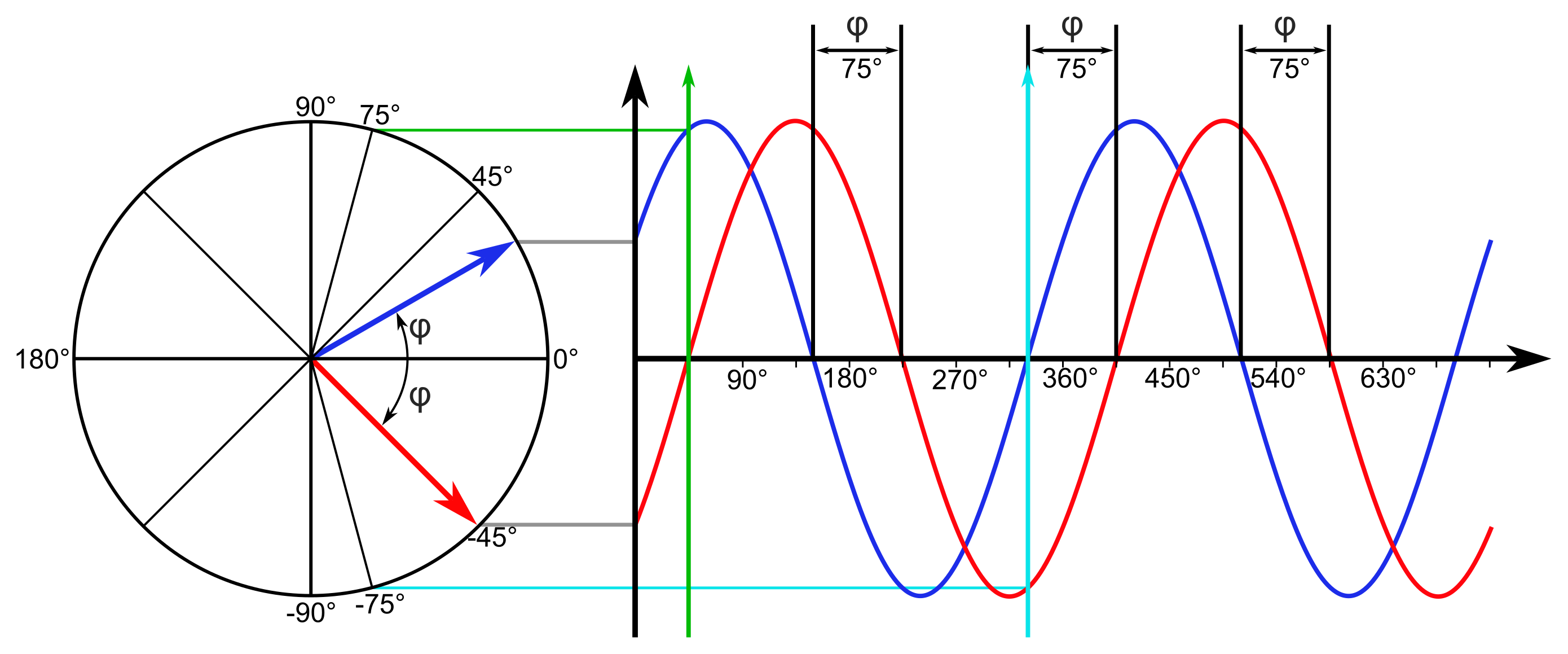
In dem Beispiel ist nicht angegeben, welcher Graph der Strom und welcher die Spannung darstellt. Wäre der blaue Graph der Strom, so wäre er der Bezugswinkel und der Phasenverschiebungswinkel -75°, was bedeutet, dass die Spannung dem Strom um 75° nacheilt.
Der komlexe Widerstand Z oder auch Impedanz genannt, lässt sich aus dem Quotienten der komplexen Spannung und dem komplexen Strom berechnen:
\( Z=\frac{U}{I}\)
Dies ist die sogenannte Polardarstellung, mittels eines Betrages und eines Winkel.
Dies ist die karthesische Darstellung, wobei man direkt den Realteil (R) und den Imaginärteil (X) ablesen kann. und somit den Wirk- und den Blindwiderstand.
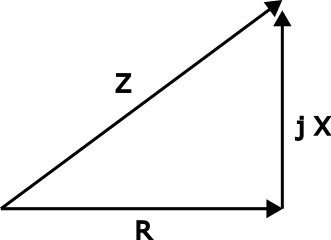
Der Scheinwiderstand berechnet sich mithilfe des Satzes des Pythagoras:
\( Z=\sqrt{R^2+X^2} \)
Der Winkel \( \varphi \) lässt sich über den Tangens berechnen:
\( arctan(\frac{X}{R}) \)
Je nachdem ob der Blindwidestand induktiv oder kapazitiv wirkt, zeigt der Zeiger des Blindwiderstandes nach oben oder unten:
Beispiel einer Reihenschaltung aus einem (Wirk-)Widerstand und einer Spule.
Beispiel aus einem (Wirk-)Widerstand und einem Kondensator.